En el año 2013 el científico matemático Ian Steward publicó un libro que contenía las “17 ecuaciones que cambiaron el mundo”.
En la actualidad las matemáticas se encuentran en nuestro alrededor aunque no nos demos cuenta, desde lo más simple de comprender hasta lo más complejo.
A continuación te contamos de qué se trata cada una de las 17 ecuaciones que cambiaron el mundo y que han sido heredadas al mundo actual.
17 Ecuaciones que cambiaron al Mundo

1.- Teorema de Pitágoras

El teorema de Pitágoras es una fórmula matemática que se usa en triángulos rectángulos para calcular la longitud de uno de los lados, llamado hipotenusa.
Un triángulo rectángulo tiene un ángulo recto, que forma un ángulo de 90 grados, y dos lados que lo rodean, llamados catetos. La hipotenusa es el lado opuesto al ángulo recto y es el lado más largo en un triángulo rectángulo.
La fórmula del teorema de Pitágoras dice que el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos. O sea, que si tenemos un triángulo rectángulo con catetos de longitud a y b, y queremos encontrar la longitud de la hipotenusa (c), podemos usar la fórmula:
c² = a² + b²
Luego, para encontrar la longitud de la hipotenusa, simplemente sacamos la raíz cuadrada de ambos lados de la ecuación:
c = √(a² + b²)
¡Así de fácil! El teorema de Pitágoras se utiliza en muchos campos, como la arquitectura, la ingeniería, la física y la geometría, y es una herramienta muy útil para resolver problemas matemáticos relacionados con triángulos rectángulos.
2.- Logaritmos
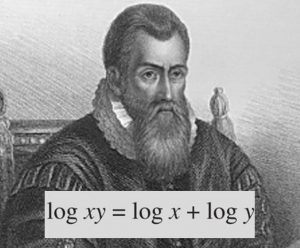
Los logaritmos son una herramienta matemática que se utilizan para simplificar cálculos y expresar grandes números de manera más sencilla. En esencia, los logaritmos son el exponente al cual debemos elevar una base específica para obtener un número determinado.
Por ejemplo, si tenemos la ecuación log2(8) = 3, esto significa que 2 elevado a la tercera potencia es igual a 8. Es decir, 2 x 2 x 2 = 8.
Los logaritmos tienen muchas aplicaciones en la vida real, especialmente en campos como la ciencia, la ingeniería, la economía y la tecnología. Algunos ejemplos de aplicaciones prácticas de los logaritmos son:
- En la acústica: los logaritmos se utilizan para medir la intensidad del sonido en decibelios (dB), lo que permite comparar el sonido de dos fuentes diferentes de manera más precisa.
- En la economía: los logaritmos se utilizan para medir la tasa de crecimiento de los precios y las ganancias a lo largo del tiempo.
- En la ingeniería: los logaritmos se utilizan para calcular la magnitud de las fuerzas y las tensiones en estructuras y materiales, lo que permite diseñar edificios, puentes y otras estructuras de manera más segura.
- En la tecnología: los logaritmos se utilizan en la compresión de datos, lo que permite almacenar y transmitir grandes cantidades de información en un espacio más pequeño.


3.- Cálculo

Hace referencia al resultado correspondiente a la acción de calcular o contar. Calcular, por su parte, consiste en realizar las operaciones necesarias para prever el resultado de una acción previamente concebida, o conocer las consecuencias que se pueden derivar de unos datos previamente conocidos.
El cálculo de Newton es una rama de las matemáticas que se enfoca en el estudio del cambio y la tasa de cambio en las funciones. Es una herramienta esencial en la física, la ingeniería, la economía, la estadística y muchas otras áreas de la ciencia.
El cálculo de Newton se divide en dos partes: el cálculo diferencial y el cálculo integral. El cálculo diferencial se utiliza para encontrar la tasa de cambio de una función en un punto dado, mientras que el cálculo integral se utiliza para encontrar la cantidad total de cambio en una función en un intervalo determinado.
A continuación, se presentan algunas aplicaciones prácticas del cálculo de Newton:
- Cálculo de la velocidad y la aceleración: se utiliza para calcular la velocidad y la aceleración de un objeto en movimiento. En física, estas medidas son fundamentales para entender el movimiento de los cuerpos y predecir su trayectoria.
- Optimización de funciones: se utiliza para encontrar los valores máximos o mínimos de una función. En la economía, por ejemplo, se utiliza para maximizar los beneficios de una empresa o minimizar los costos de producción.
- Modelado matemático: se utiliza para modelar y simular sistemas complejos. En la ingeniería, por ejemplo, se utiliza para modelar el flujo de líquidos en una tubería o el movimiento de un objeto en el espacio.
- Análisis de datos: se utiliza en la ciencia de datos para analizar y predecir patrones en conjuntos de datos. Por ejemplo, se puede utilizar para ajustar una curva a un conjunto de datos y predecir futuros valores.
- Diseño de sistemas de control: se utiliza en la ingeniería para diseñar sistemas de control. Por ejemplo, se puede utilizar para diseñar un sistema de control automático para mantener la temperatura constante en una habitación.
- Cálculo de integrales: el cálculo de Newton se utiliza para calcular integrales, que son fundamentales en la física, la ingeniería y otras disciplinas. Por ejemplo, se utiliza para calcular la cantidad de trabajo realizado por una fuerza a medida que se mueve un objeto.
4.- Ley de la Gravedad
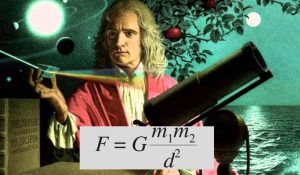
La ley de la gravedad, también conocida como ley de gravitación universal, establece que cada cuerpo en el universo atrae a cualquier otro cuerpo con una fuerza que es proporcional a las masas de los cuerpos y a la distancia entre ellos. Esta ley fue descubierta por Sir Isaac Newton en el siglo XVII y se ha convertido en una de las leyes fundamentales de la física.
La ley de la gravedad tiene numerosas aplicaciones prácticas en la civilización, entre ellas:
- Astronomía: Para entender y predecir el movimiento de los planetas, satélites y otros objetos en el espacio. Por ejemplo, la ley de la gravedad se utiliza para calcular la órbita de la Tierra alrededor del Sol.
- Geología: Para estudiar la estructura interna de la Tierra. Los geólogos utilizan mediciones de la gravedad para identificar cambios en la densidad y la composición de la corteza terrestre.
- Navegación: Para calcular la posición y el movimiento de los barcos y aviones. Los sistemas de navegación modernos utilizan mediciones de la gravedad para determinar la altura y la velocidad de un objeto.
- Ingeniería: En la construcción de edificios y puentes. Los ingenieros utilizan la gravedad para calcular la carga que soportarán las estructuras y para diseñar sistemas de drenaje y alcantarillado.
- Comunicaciones: Para calcular la posición de los satélites y para predecir el movimiento de los cuerpos celestes. Esto es esencial para la comunicación satelital y para la navegación por GPS.
5.- La raíz cuadrada de menos uno

Los números ordinarios y corrientes, ‘la raíz cuadrada de menos uno’ no existe. Sin embargo, los matemáticos encuentran útil inventar un completamente nuevo tipo de número para cumplir ese papel. Ellos decidieron asumir que dicha raíz realmente existió, escribiendo la ‘i’ para representarla. (La letra ‘i’ fue escogida porque es de “imaginario”).
La fórmula de la raíz cuadrada de menos uno se conoce como el número imaginario “i”. Esta fórmula tiene aplicaciones en la civilización en diversas áreas, como la matemática, la física, la ingeniería y la electrónica. Algunas de sus aplicaciones son:
- Matemáticas: La fórmula de la raíz cuadrada de menos uno se utiliza en matemáticas para resolver ecuaciones cuadráticas y otras ecuaciones complejas. También es útil en el estudio de funciones complejas, como las funciones trigonométricas y exponenciales complejas.
- Física: Se utiliza en la física para describir fenómenos ondulatorios, como la propagación de ondas electromagnéticas en el espacio. Además, se utiliza para describir la polarización de la luz y otros fenómenos ópticos.
- Ingeniería: Se utiliza en ingeniería eléctrica para describir las señales de corriente alterna, como las ondas sinusoidales y las señales de radio. También se utiliza en la teoría de control y en la ingeniería de sistemas, para analizar y diseñar sistemas complejos.
- Electrónica: Se utiliza en electrónica para describir la respuesta de los circuitos eléctricos a las señales de entrada. También se utiliza en el análisis y diseño de filtros electrónicos y otros dispositivos electrónicos complejos.
6.- Fórmula de Euler para Poliedro
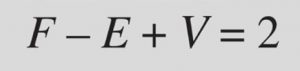

La fórmula de Euler para poliedros es una relación matemática que se utiliza para describir la relación entre el número de vértices, aristas y caras en un poliedro. Esta fórmula establece que para cualquier poliedro convexo, el número de vértices (V), menos el número de aristas (E), más el número de caras (F), es siempre igual a 2. Es decir, V – E + F = 2.
Tiene diversas aplicaciones prácticas en la civilización, entre ellas:
- Geometría: Para clasificar y describir los diferentes tipos de poliedros, como los sólidos platónicos, los poliedros regulares y los poliedros arquimedianos. También se utiliza en la construcción y diseño de poliedros, como en la creación de modelos arquitectónicos y estructurales.
- Topología: En la topología para estudiar las propiedades de las superficies y objetos tridimensionales. Por ejemplo, se utiliza para analizar las propiedades de las superficies curvas, como las esferas y los toroides.
- Ingeniería: En la ingeniería para analizar y diseñar estructuras tridimensionales, como los puentes y los edificios. También se utiliza para analizar la estabilidad y resistencia de las estructuras ante cargas externas.
- Informática: En la informática para modelar y diseñar objetos tridimensionales en el diseño gráfico, animación y realidad virtual. También se utiliza en la creación de algoritmos para el procesamiento de imágenes y reconocimiento de formas.
7.- Distribución normal
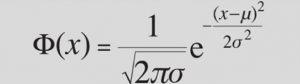
La distribución normal o distribución de Gauss es una distribución de probabilidad continua que se utiliza para modelar muchos fenómenos naturales y sociales en los que los datos se distribuyen alrededor de una media central. Esta distribución se caracteriza por una forma de campana simétrica y se describe completamente por dos parámetros: la media y la desviación estándar.
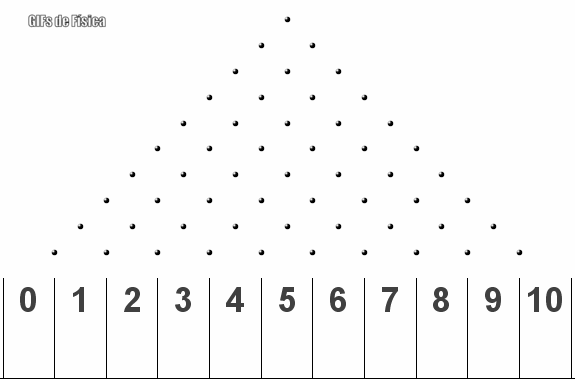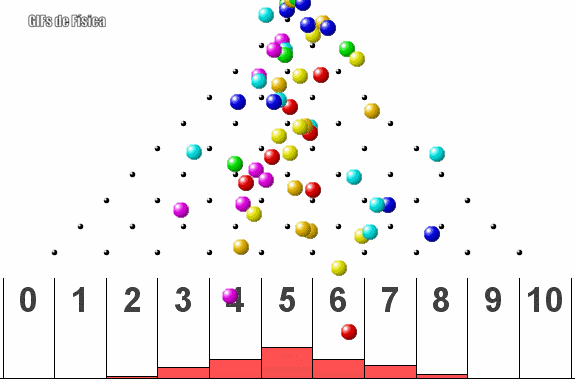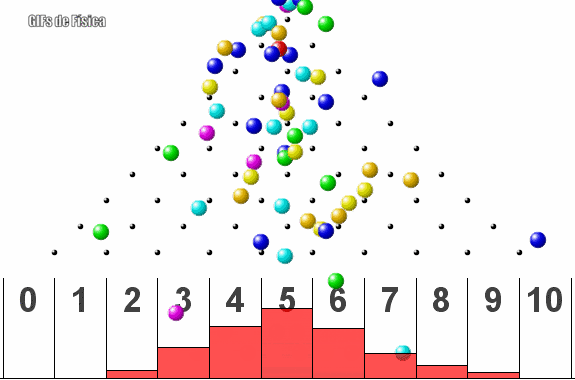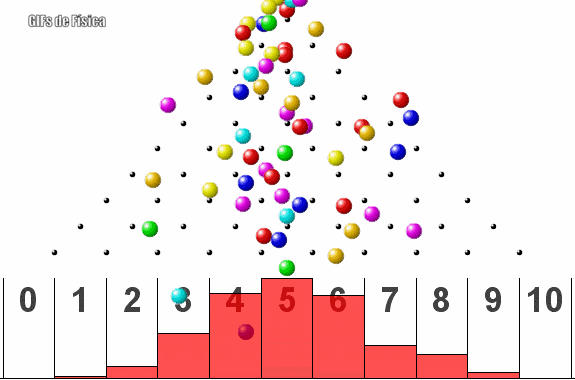
La distribución normal tiene diversas aplicaciones prácticas en el desarrollo de la civilización, entre ellas:
- Estadística: La distribución normal es una herramienta fundamental en la estadística, ya que se utiliza para modelar y analizar datos cuantitativos en diversas áreas, como la economía, la psicología y la biología. Se utiliza para describir la distribución de datos en una población y para calcular probabilidades de eventos aleatorios.
- Ingeniería: Para el diseño de sistemas y productos, ya que permite analizar y predecir la variabilidad de los procesos y los productos. Por ejemplo, se utiliza en la ingeniería de calidad para analizar la calidad de los productos manufacturados y para mejorar los procesos de producción.
- Finanzas: Para modelar y analizar los rendimientos de las inversiones y los riesgos financieros. Se utiliza en la valoración de opciones y en el análisis de carteras de inversión.
- Medicina: Para analizar y modelar los resultados de las pruebas médicas y para evaluar los efectos de los tratamientos médicos. Se utiliza para analizar la distribución de las medidas de la salud en la población, como la altura y el peso.
8.- Ecuación de Onda
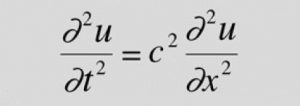
La ecuación de onda es una ecuación diferencial parcial que describe cómo se propagan las ondas en el tiempo y el espacio. Se utiliza para modelar una amplia variedad de fenómenos ondulatorios, como las ondas sonoras, las ondas electromagnéticas, las ondas sísmicas y las ondas en el agua.
Sus usos principales en el desarrollo de la civilización son:
- Comunicaciones: Para modelar y analizar las señales electromagnéticas que se propagan en el espacio. Se utiliza en la ingeniería de telecomunicaciones para diseñar y optimizar las redes de comunicaciones y para desarrollar nuevas tecnologías de comunicación.
- Acústica: Para modelar y analizar las ondas sonoras que se propagan en el aire y otros medios. Se utiliza en la ingeniería acústica para diseñar y optimizar los sistemas de sonido y para desarrollar nuevas tecnologías de reducción de ruido.
- Geofísica: Para modelar y analizar las ondas sísmicas que se propagan en la Tierra. Se utiliza en la exploración geofísica para identificar y mapear los recursos naturales, como el petróleo y el gas.
- Medicina: Para modelar y analizar las ondas sonoras que se utilizan en la ecografía y en la terapia de ultrasonido. Se utiliza para desarrollar nuevas técnicas de diagnóstico y tratamiento médico.
9.- La transformada de Fourier
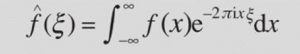
La transformada de Fourier es una herramienta matemática que permite descomponer una señal compleja en sus componentes fundamentales, es decir, en las diferentes frecuencias que la componen. Esta transformada se utiliza en diversas áreas de la ciencia y la tecnología para el análisis y procesamiento de señales, así como para el diseño de sistemas y dispositivos electrónicos.
Los usos más importantes de la transformada de Fourier para el desarrollo de la civilización son los siguientes:
- Procesamiento de señales: En el procesamiento de señales para analizar y filtrar señales de audio, vídeo, imágenes y otros tipos de señales. Por ejemplo, se utiliza en el procesamiento de imágenes médicas para detectar tumores y otras anomalías.
- Comunicaciones: Para analizar y diseñar sistemas de transmisión de datos. Por ejemplo, se utiliza en la modulación de frecuencia para transmitir señales de radio y televisión.
- Ingeniería eléctrica: Para analizar y diseñar circuitos electrónicos y sistemas de control. Por ejemplo, se utiliza en el diseño de filtros para sistemas de audio y en el diseño de sistemas de control de motores eléctricos.
- Matemáticas: Para resolver ecuaciones diferenciales y otras aplicaciones. Por ejemplo, se utiliza en la resolución de ecuaciones de onda y en la teoría de las funciones especiales.
10.- Ecuaciones de Navier-Stokes
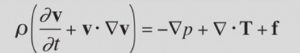
Las ecuaciones de Navier-Stokes son un conjunto de ecuaciones diferenciales parciales que describen el movimiento de fluidos, como líquidos y gases. Estas ecuaciones son importantes en la mecánica de fluidos y se utilizan para modelar una amplia variedad de fenómenos, como el flujo de aire alrededor de los aviones, la circulación de la sangre en el cuerpo humano, la generación de olas en el océano, entre otros.

Los usos más importantes de las ecuaciones de Navier-Stokes para el desarrollo de la civilización son los siguientes:
- Ingeniería aeronáutica: Para analizar el flujo de aire alrededor de los aviones y para diseñar aerodinámica más eficientes. Se utilizan para simular y predecir el comportamiento de los fluidos en torno a las estructuras de los aviones.
- Ingeniería mecánica: Para analizar el flujo de líquidos a través de tuberías, válvulas y otros componentes de sistemas hidráulicos. Se utilizan para diseñar sistemas de tuberías y válvulas más eficientes y para predecir el comportamiento de los fluidos en los sistemas hidráulicos.
- Geofísica: Para analizar la circulación oceánica y la atmósfera terrestre. Se utilizan para simular y predecir el comportamiento de los fluidos en los océanos y la atmósfera.
- Medicina: Para analizar el flujo sanguíneo en el cuerpo humano y para diseñar prótesis vasculares. Se utilizan para simular y predecir el comportamiento de los fluidos en el sistema circulatorio humano.
11.- Ecuaciones de Maxwell
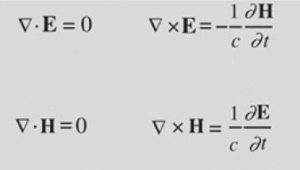
Las ecuaciones de Maxwell son un conjunto de cuatro ecuaciones diferenciales parciales que describen el comportamiento de los campos electromagnéticos, es decir, el campo eléctrico y el campo magnético, en presencia de fuentes como cargas eléctricas y corrientes eléctricas. Estas ecuaciones son fundamentales en el estudio de la electricidad y el magnetismo y tienen una gran cantidad de aplicaciones prácticas.
Los usos más importantes de las ecuaciones de Maxwell en el desarrollo de la civilización son los siguientes:
- Tecnología de la información y las comunicaciones: Por ejemplo, se utilizan en la teoría de las ondas electromagnéticas, que es la base de las tecnologías de radio, televisión, telefonía móvil, internet, entre otros.
- Ingeniería eléctrica y electrónica: Para diseñar y analizar dispositivos como transformadores, motores eléctricos, generadores, circuitos eléctricos y electrónicos, entre otros.
- Medicina: Para el diseño y análisis de tecnologías de diagnóstico médico, como resonancias magnéticas y tomografías computarizadas.
- Energías renovables: En la generación y distribución de energía eléctrica a partir de fuentes renovables como la energía solar y la energía eólica. Por ejemplo, se utilizan en el diseño y análisis de sistemas de paneles solares y turbinas eólicas.
- Investigación científica: Las ecuaciones de Maxwell también tienen importantes usos en la investigación científica, en campos como la física, la química, la biología, entre otros.
12.- Segunda Ley de la Termodinámica
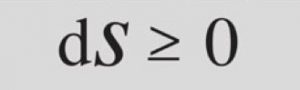
La Segunda Ley de la Termodinámica es uno de los principios fundamentales de la física que describe la irreversibilidad de los procesos termodinámicos en el universo. En su formulación más común, la Segunda Ley establece que el calor fluye espontáneamente de una región de alta temperatura a una región de baja temperatura, y que no es posible transformar completamente el calor en trabajo útil sin generar alguna forma de entropía (una medida de la cantidad de desorden o degradación de la energía en un sistema).

Las aplicaciones más importantes de la Segunda Ley de la Termodinámica en el desarrollo de la civilización son las siguientes:
- Producción de energía: Fundamental en la producción de energía en las centrales termoeléctricas, donde se aprovecha la energía térmica para generar electricidad. También es esencial en la producción de energía renovable, como la energía solar y eólica.
- Diseño de motores: Esencial en el diseño de motores, como los motores de combustión interna, turbinas y motores eléctricos. La eficiencia de estos motores está limitada por la Segunda Ley, ya que no es posible transformar completamente el calor en trabajo útil.
- Refrigeración: Los sistemas de refrigeración y aire acondicionado aprovechan la transferencia de calor desde un medio frío a uno caliente, lo que requiere trabajo y genera entropía.
- Tecnología de materiales: Limita la eficiencia en la producción y procesamiento de materiales y aleaciones, como en la producción de acero.
- Biología: Establece que cualquier proceso biológico es irreversible y genera entropía. Por ejemplo, la respiración y la digestión son procesos que transforman la energía química en trabajo útil, pero generan entropía en el proceso.
13.- La Teoría de la Relatividad
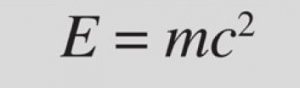
La Teoría de la Relatividad es una teoría física desarrollada por Albert Einstein en el siglo XX que describe cómo se comporta la materia y la energía en el universo, especialmente a velocidades cercanas a la velocidad de la luz. La Teoría de la Relatividad se divide en dos partes: la Relatividad Especial, que describe el comportamiento de objetos en movimiento uniforme, y la Relatividad General, que describe la relación entre la materia y la gravedad.
Las aplicaciones más importantes de la Teoría de la Relatividad en el desarrollo de la civilización son las siguientes:
- Sistemas de navegación GPS: Esencial en el funcionamiento de los sistemas de navegación GPS, ya que los satélites de GPS deben tomar en cuenta las diferencias en el tiempo medido en la Tierra y en el espacio debido a la dilatación del tiempo prevista por la Teoría de la Relatividad.
- Tecnología de los aceleradores de partículas: Se utiliza para describir el comportamiento de las partículas subatómicas que se aceleran a velocidades cercanas a la velocidad de la luz.
- Energía nuclear: Describe cómo se produce la energía en las reacciones nucleares y cómo se convierte la masa en energía, como se describe en la famosa ecuación E=mc^2.
- Astronomía: Describe el comportamiento de la luz en el espacio y cómo se curva en presencia de campos gravitatorios intensos, como los producidos por estrellas y galaxias.
- Tecnología de la comunicación: Describe cómo se comportan las ondas electromagnéticas, como las ondas de radio y la luz, en el espacio y en presencia de campos gravitatorios.
14.- Ecuación de Schrödinger
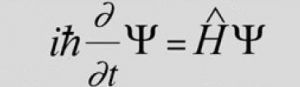
La ecuación de Schrödinger es una ecuación fundamental en la física cuántica que describe la evolución temporal de la función de onda de un sistema cuántico. Fue propuesta por el físico austríaco Erwin Schrödinger en 1925 y es una de las bases teóricas de la mecánica cuántica.
La ecuación de Schrödinger se utiliza para describir el comportamiento de los sistemas cuánticos, como los átomos, las moléculas y las partículas subatómicas. Su formulación matemática es compleja, pero se puede resumir en términos generales como una ecuación que describe cómo cambia la función de onda de un sistema cuántico en el tiempo.
Las aplicaciones más importantes de la ecuación de Schrödinger en el desarrollo de la civilización son las siguientes:
- Electrónica y tecnología de semiconductores: La ecuación de Schrödinger se utiliza para describir el comportamiento de los electrones en materiales semiconductores, como los utilizados en la electrónica y la informática, y es esencial para el diseño y la fabricación de dispositivos electrónicos como transistores, diodos y circuitos integrados.
- Química y materiales: Se utiliza para describir la estructura y la dinámica de las moléculas y los materiales a nivel molecular, lo que es esencial para la química y la ciencia de materiales y para el diseño de nuevos materiales y medicamentos.
- Física de partículas: Se utiliza en la física de partículas para describir el comportamiento de las partículas subatómicas, como los electrones, los protones y los neutrones, y es esencial para la comprensión de la estructura y la dinámica de los núcleos atómicos.
- Criptografía cuántica: Es una forma de criptografía que utiliza los principios de la mecánica cuántica para garantizar la seguridad de la información.
15.- Teoría de la Información
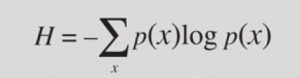
La teoría de la información es una rama de las matemáticas y la informática que se ocupa del procesamiento, almacenamiento y transmisión de información. Fue desarrollada por el matemático estadounidense Claude Shannon en la década de 1940 y se ha convertido en un campo de estudio esencial para la tecnología de la información y la comunicación modernas.
La teoría de la información se centra en la medición y la cuantificación de la información, la eficiencia de los sistemas de comunicación y la capacidad de los sistemas para detectar y corregir errores. Sus aplicaciones más importantes en el desarrollo de la civilización son las siguientes:
- Telecomunicaciones: La teoría de la información se utiliza en el diseño y la optimización de sistemas de comunicación, como las redes de telefonía, la televisión por cable, la transmisión de datos por internet, entre otros.
- Compresión de datos: Se utiliza en la compresión de datos para reducir el tamaño de los archivos de datos sin perder información importante. Es esencial para la transmisión y el almacenamiento eficientes de grandes cantidades de datos, como imágenes, videos, música y documentos.
- Criptografía: La teoría de la información se utiliza en la criptografía, que es el estudio de los algoritmos y protocolos que garantizan la seguridad de la información. Es esencial para la seguridad en la transmisión y almacenamiento de datos sensibles, como información financiera, médica o gubernamental.
- Inteligencia artificial: Para la clasificación de datos, el procesamiento del lenguaje natural y el reconocimiento de patrones. Es esencial para el desarrollo de aplicaciones como los sistemas de recomendación, los chatbots y los asistentes virtuales.
16.- Teoría del caos
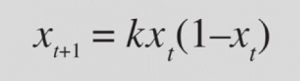
La teoría del caos es un campo de estudio interdisciplinario que se centra en sistemas dinámicos complejos y no lineales que parecen ser altamente sensibles a pequeñas variaciones en las condiciones iniciales. Esta teoría se ocupa de la comprensión de los patrones emergentes y la impredecibilidad en sistemas dinámicos, como el clima, la biología, la economía, la física y muchos otros.
Aunque a menudo se asocia con la idea de “caos” o desorden, la teoría del caos también aborda los patrones subyacentes y la estructura inherente de los sistemas complejos. Algunos de los usos más importantes de la teoría del caos en el desarrollo de la civilización son los siguientes:
- Meteorología: Se utiliza en la predicción del clima y la meteorología. Al entender cómo pequeñas variaciones en las condiciones iniciales pueden tener un gran impacto en el resultado final, los científicos pueden mejorar la precisión de las predicciones del clima.
- Economía: Para entender cómo pequeñas perturbaciones pueden desencadenar grandes cambios en los mercados financieros y económicos. También se utiliza en la predicción de tendencias del mercado y en la evaluación del riesgo financiero.
- Biología: Para entender los patrones emergentes en los sistemas biológicos, como la propagación de enfermedades, la evolución de especies y el comportamiento de las poblaciones animales.
- Física: Para entender los sistemas no lineales y los fenómenos complejos, como la turbulencia, la dinámica de los fluidos y la propagación de ondas.
- Ingeniería: Para mejorar el diseño y la optimización de sistemas complejos, como los sistemas de control de procesos, las redes de comunicación y los sistemas de transporte.
17.- Ecuación de Black-Scholes
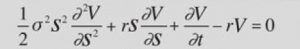
La ecuación de Black-Scholes es una fórmula matemática utilizada en finanzas para determinar el precio teórico de una opción financiera, tomando en cuenta factores como el precio actual del activo subyacente, la tasa libre de riesgo, la volatilidad del precio del activo y el tiempo restante hasta la expiración de la opción.
La ecuación de Black-Scholes fue desarrollada en 1973 por los economistas Fischer Black y Myron Scholes, y se ha convertido en un modelo ampliamente utilizado en finanzas para calcular el precio de opciones sobre acciones, bonos y otros tipos de activos financieros. Es considerada una de las contribuciones más importantes de la teoría financiera moderna.
Los usos más importantes de la ecuación de Black-Scholes en el desarrollo de la civilización son los siguientes:
- Valoración de opciones: Al proporcionar una fórmula precisa para el precio teórico de una opción, la ecuación permite a los inversores y a las empresas calcular el valor de sus opciones y tomar decisiones informadas sobre cómo invertir su capital.
- Gestión de riesgos: Al proporcionar una forma precisa de calcular el precio de una opción, la ecuación permite a los inversores y a las empresas identificar y gestionar mejor los riesgos asociados con la inversión en opciones.
- Investigación financiera: La ecuación de Black-Scholes ha sido utilizada en una gran cantidad de investigaciones financieras y académicas. Ha sido ampliamente estudiada y ha dado lugar a numerosas variaciones y mejoras en la teoría financiera moderna.
- Desarrollo de instrumentos financieros: La ecuación de Black-Scholes ha sido utilizada para desarrollar nuevos tipos de instrumentos financieros, como las opciones exóticas y las opciones binarias.


Pingback: Ecuaciones que cambiaron el Mundo y sus aplicaciones en la Civilización – El Portu 11